5054 Physics Random Questions [2]

Physics 5054

Random Question Samples
Structured Question

[Below are sample responses to the questions in this link. Consider answering questions in the link first and then look at these responses.]

1. Indira’s  train is at rest in a railway station. 

At time t = 0, the train starts to move forwards with an increasing speed until it reaches its maximum speed at time t = 48 s.

Fig. 1.1 is the speed-time graph for the first 48 s of the journey.

Fig. 1.1

(a) (i)      State how the graph shows that, during the first 48 s of the journey, the 

        acceleration of the train is constant.

The gradient [or change in speed over change in time] of the graph is constant. [1] 

(ii) Calculate the acceleration of the train during the first 48 s of the journey.

 a =  Δv /  Δt

a = (36 m/s - 0) / (48 s - 0)

a = 0.75 m/s2

acceleration = a = 0.75 m/s2 [2] 

(b) After time t = 48 s, the train continues at its maximum speed for another 72 s.

(i) On Fig. 1.1, sketch the speed-time graph for the next 72 s of the journey.  

(See the orange line in Fig. 1.1.) [1] 

(ii) Determine the total distance travelled by the train in the 120 s after it starts             moving.

The distance is the area under the speed-time graph.

distance = area of triangle + area of rectangle

distance = 3500 m [3] 

[Total: 7]

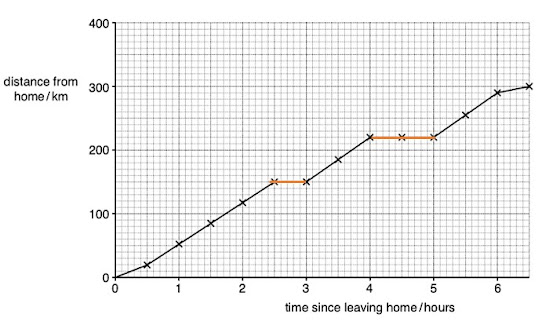
2. Valene goes for holiday vacation in a car. Every half an hour she notes down the distance she has travelled since she left home. She then plots the graph shown in Fig. 2.1.

 

Fig. 2.1

The first half hour and the last half hour of her journey are on small roads. The rest of the journey is on major roads.

Answer the following questions using information from Fig. 2.1.

(a)     For how many hours was she travelling on major roads?

The graph shows 6.5 hours journey. But two 30-minute of it were on small roads.

Valene, therefore, only spent 5.5 hours on major roads.

NOTE: You may answer 4 hours also as there are 1.5 hours when she was not moving on major roads.

time = 5.5 [or 4.0] hours [1]

(b)    How far did she travel

(i)     in total,

The answer can easily seen from the vertical axis [distance] in the graph.

total distance = 300 km

(ii)     on small roads,

distance on small roads = 30 km

(iii)     on major roads?

distance on major roads = 270 km [3]

(c)     She had two refreshment stops whilst on the journey.

          On Fig. 2.1, clearly mark where she had these stops.       

(See the orange marks in Fig. 2.1.) [1]

(d)      Apart from the times when she stopped, during which section of the journey was her speed slowest? 

            

         Explain your answer.

section Speed is slowest at the last section

explanation In a distance-time graph, speed is the gradient. The last section has the smallest gradient

2]

(e)     Calculate the average speed, in m/s, for the whole journey. 

Average speed = total distance / total time

Average speed = 300 m / 6.5 s

average speed = 46 km/h [4] 

[Total: 11]

3. Fig. 3.1 shows a model fire engine designed by Pavithra to take measurements of force and motion.

Fig. 3.1

The model projects a jet of water forwards. The forcemeter holds the model stationary. It indicates a force of 0.060 N acting on the model.

The forcemeter is now disconnected and the model accelerates to the right at 0.030 m/s2.

(a)      The back of the model breaks a pair of light beams and the time to pass between them is measured electronically. The beams are 12 mm apart and the second beam is broken 0.080 s after the first.

Pavithra times with a stopwatch how long it takes from the release of the model until the beams are cut.

Calculate the time she measures.

acceleration a =  Δv / t

or a = (v - u) / t

Therefore, the time t can be calculated by

t = (v - u) / a

NOTE:

• when a [=0.030 m/s2] and u [= 0] are given, v is not 

•  but v can be calculated using d/t
• d = 12 mm
• t = 0.080 s
• v = 150 mm/s or 0.15 m/s

 t = (0.15 m/s - 0) / 0.030 m/s2

t = 5.0 s

 

time measured = 5.0 s [4]

(b)       This experiment is carried out with the water tank in the model nearly full. 

Calculate the mass of the model including the water in the tank.

Newton's 2nd Law:

a = F / m

m = F / a

m = 0.60 N / 0.030 m/s2

m = 2.0 kg

mass = 2.0 kg [2]

(c)      She repeats the experiment with the same force but with the water tank nearly empty.

State and explain how the acceleration will compare to that of the first experiment. 

There will be greater acceleration because the mass is less. Acceleration is inversely proportional to mass when force is held constant.

[2]

[Total: 8]

4. Fig. 4.1 shows Aahan pushing a heavy box with a force P. 

A frictional force F acts in a horizontal direction.

Fig. 4.1

(a) The forces on the box are balanced and the box is stationary.

(i)       State what is meant by balanced forces. 

Balanced force means the sum of equal and opposite forces acting on an object. The resultant force is zero.

[1] 

(ii)       Apart from being stationary, describe one other possible state of motion of 

the box when the forces are balanced. 

A motion at constant velocity or constant speed along a straight line.

[1]

 (b)      When P = 100 N and F = 85 N, the box accelerates. The mass of the box is 25 kg. 

Calculate the acceleration of the box. 

resultant force = 100 N - 85 N

resultant force = 15 N

acceleration = resultant force / mass

acceleration = 15 N / 25 kg

acceleration = 0.60 m/s2 [2] 

[Total: 4]